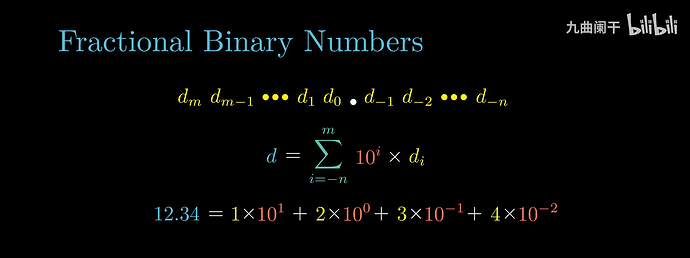注:你可以在 Github 仓库中获取 Markdown 原文,也可以在 Github Pages 上阅读该文章
2.信息的表示和处理
信息的存储
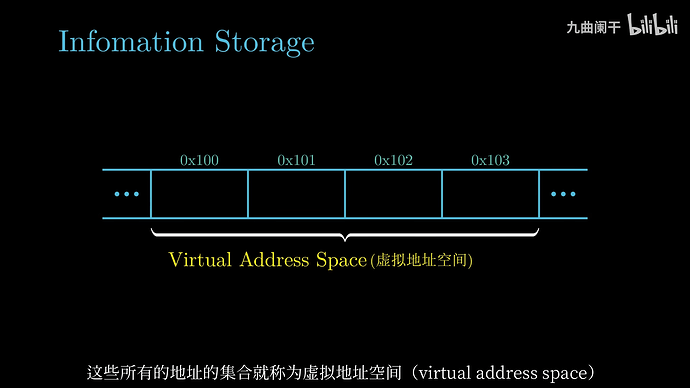
通常情况下,程序将内存视为一个非常大的数组,数组的元素由一个个字节组成,每个字节都有唯一的数字表示,称为 Address(地址),所有地址的集合就称为 Virtual Address Space(虚拟地址空间)
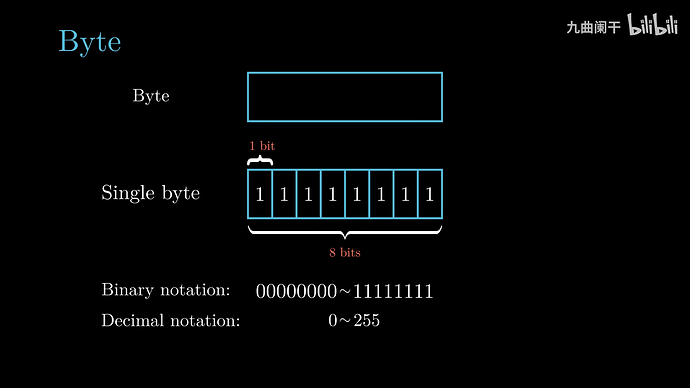
word size(字长): 决定了虚拟地址空间的大小,字长为 w 位的机器的虚拟地址空间 (程序使用连续的虚拟地址访问内存/磁盘) 的范围是 0 \sim 2^{w} - 1 (因为每一个 bit 位有 0 和 1 两种取值)
- 32 位系统(如 x86)的虚拟地址空间最大为 4GB( 2^{32} Byte)
- 64 位系统(如 x86_64):理论上可支持 16EB( 2^{64} Byte),但实际操作系统通常不会完全使用。例如:
- Linux 默认使用 48 位地址空间(256TB)。
- Windows 也类似,通常使用 47-48 位地址。
大多数 64 位机器向后兼容,可以运行 32 位程序
32 位程序与 64 位程序的区别是编译过程,而不是运行机器的类型
在编译时可以通过编译选项指定生成 32 位的程序还是 64 位的程序
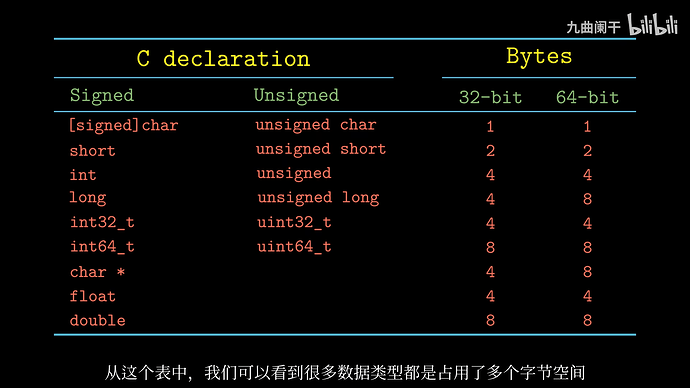
不同的数据类型可能占用不同的大小,同时对于不同位数的机器也有区别,很多数据类型都是占用了多个字节空间
对于需要存储的数据,我们需要知道「该数据的地址是什么」以及「数据在内存中是如何排布的」
Byte Ordering(字节序):数据在内存中的排列形式,有大端法与小端法两种方式,区别在于高位地址的位置
- Big Endian(大端法): 高位有效字节存储在低地址处 (优先读取最高有效字节),更符合人类直觉,适用于网络传输和存储
- Little Endian(小端法): 低位有效字节存储在低地址处 (优先读取最低有效字节),适合计算机内部处理,主流 CPU 采用
| 字节序 | 定义 | 示例(0x12345678) | 常见用途 |
|---|---|---|---|
| Big Endian | 高位字节存低地址 | 12 34 56 78 |
网络通信(TCP/IP)、部分 RISC 处理器(PowerPC、SPARC)、部分文件格式 |
| Little Endian | 低位字节存低地址 | 78 56 34 12 |
x86、ARM 默认模式、Windows/Linux 处理 |
32 位机器使用 4 字节地址,64 位机器使用 8 字节地址 (这对应了指针的占用大小)
字符串的表示:在 C 语言中,使用 NULL(‘\0’) 作为一个字符串的结尾标识。比如要存储 “abcde”,虽然只有 5 个字符,但是长度却是 6
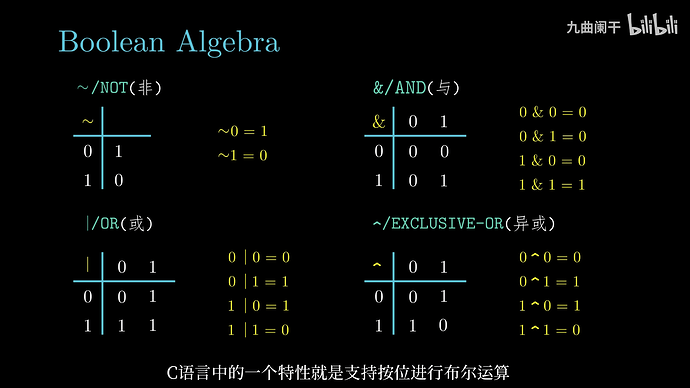
布尔代数:逻辑运算推理,如与 (and)、非 (or)、或 (not)、异或 (xor)
位级运算: 一个常见用途就是实现掩码运算
逻辑运算: 零表示 false,非零表示 true
移位运算: 左移在低位补 0 即可;右移分为逻辑右移与算术右移,Java 中的 >>> 专门提供了逻辑右移
- 逻辑右移:高位补 0
- 算数右移:高位补符号位(有符号数在进行右移时,需要使用算数右移)
整数 Integer
整数的表示
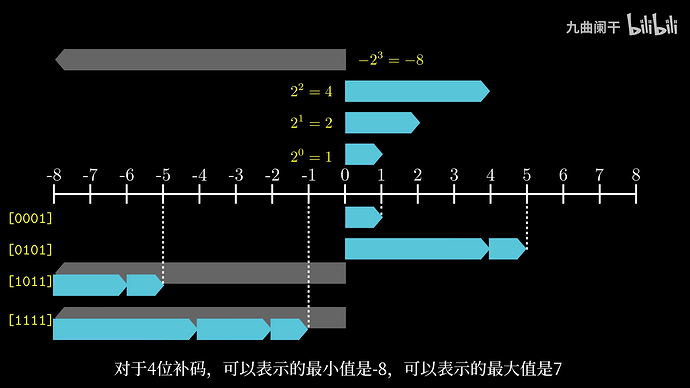
计算机中对于有符号数的编码采用补码 (Two’s Complement) 的形式,最高位作为符号位
关于符号位,需要理解负权重的概念,而不能简单的当成一个负号
无符号数和有符号数的区别在于有没有最高位的符号位,以及由此带来的计算方式的不同。符号位中,0 标识了非负数,1 标识了负数(原因是最高位的负权重一定大于其余位的和)
类型转换
对于 C 语言,在进行有符号和无符号数的互相转换时:
- 具体每一个字节的值不会改变,改变的是计算机解释当前值的方式
- 如果一个表达式既包含有符号数也包含无符号数,那么会被隐式转换成无符号数进行比较(这个隐式转换可能导致意想不到的问题)
C 语言中的隐式类型转换可能会导致意想不到的问题,因此很多语言在编译时禁止了不同类型间的比较和运算,如 Go 语言
类型扩展与截取
- 扩展(例如从
short int到int),保持数值不变是可以的,书中给出了数学证明- 无符号数:零扩展,在扩展的数位补 0
- 有符号数:符号位扩展,在扩展的位数补符号位的数值(即最高位)
- 截取(例如
unsigned int到unsigned short),想要保持数据不变只有在小数据的情况下是可能的(原数本身在目标位宽内)- 无符号数:丢弃多出的高位,相当于取模运算
- 有符号数:同样截断,再重新解释。
- 如 -41,8 位的二进制表示是
1101 0111,在截取 4 位后,无法表示原数(因为 4 位补码可表示的范围是 –8 到 7)
- 如 -41,8 位的二进制表示是
当两个不同数据类型进行比较或者运算时,C 语言会自动做拓展(如果可以),把小的数据类型转换成大的
正数加减法运算
- 溢出丢弃:如果两个 w 位的数字相加,结果是 w+1 位,则会丢弃最高位(实际上是做了一个取模操作)
- 两个无符号数相加,可能因为溢出导致结果更小
- 两个有符号数相加,操作和无符号数相同,只是解释时不同,分为正溢出和负溢出
- 正溢出 (positive overflow):数值太大,符号位的 0 变为了 1,导致解释为负数
- 如 1 字节的有符号的 127 与 1 相加,期望得到 128,但最后得到了 -128
- 负溢出 (negative overflow):数值太小,符号位的 1 变为了 0,导致解释为正数
- 如 1 字节的有符号的 -128 与 -1 相加,期望得到 -129,但最后得到了 127
- 正溢出 (positive overflow):数值太大,符号位的 0 变为了 1,导致解释为负数
- 溢出检测:C 语言中并不会对溢出进行报错
- 两个无符号数相加:当发生溢出时得到的和一定小于任何一个数(推导见图)
- 两个有符号数相加:
- 两个正数相加,得到的结果为负,则说明发生了正溢出
- 两个负数相加,得到的结果为正,则说明发生了负溢出
- 注意:一正一负相加是不会溢出的
正数乘除法运算
[!todo] 这里没有详细看
乘法同加法运算一样,当溢出时会进行截断
乘法指令的执行需要多个时钟周期,很多 C 语言编译器试图用移位、加法以及减法代替整数乘法的操作
对于除以 2 的幂也可以用移位实现(无符号数使用逻辑右移,有符号数使用算数右移)
整数除法可能遇到除不尽的情况,统一 0 舍入
浮点数 Float
[!todo] 这里没有详细看
定点表示法
可以类似于 10 进制用一个统一的公式来表达:\sum_{k = - j}^{i} b_{k} \times 2^{k}
例如 5 \frac{3}{4} = (101.11)_{2} , 2 \frac{7}{8} = (10.111)_{2} , 1 \frac{7}{16} = (1.0111)_{2}
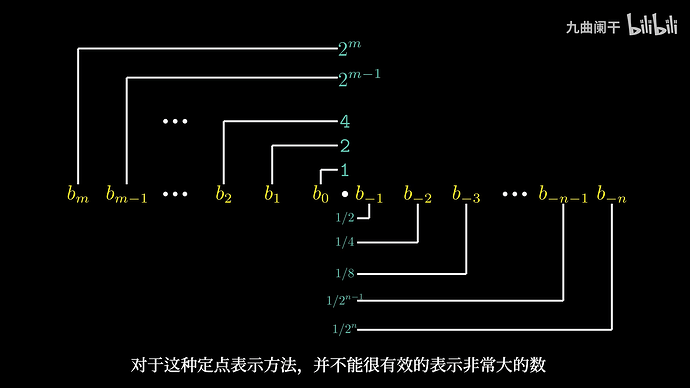
这种表达方式其实是比较明显的限制的,比如说,只有形为 \frac{x}{2^{k}} 的小数部分可以被精确表示,其他的数字会变成循环的小数,例如:\frac{1}{3} = 0.0101010101[01](\ldots)_{2}。
除此之外,另一个问题在于,如果给定了 w 个比特,能够表达的数字其实是有限的,具体的原因会在后面详细解释。
IEEE 浮点数标准
参考资料
- 【读薄 CSAPP】壹 数据表示 - 小土刀
- 【CSAPP-深入理解计算机系统】2-1.信息的存储(上) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-1.信息的存储(下) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-2.整数的表示(上) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-2.整数的表示(下) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-3.整数的运算(上) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-3.整数的运算(下) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-4.浮点数(上) - 九曲阑干
- 【CSAPP-深入理解计算机系统】2-4.浮点数(下) - 九曲阑干