请看题
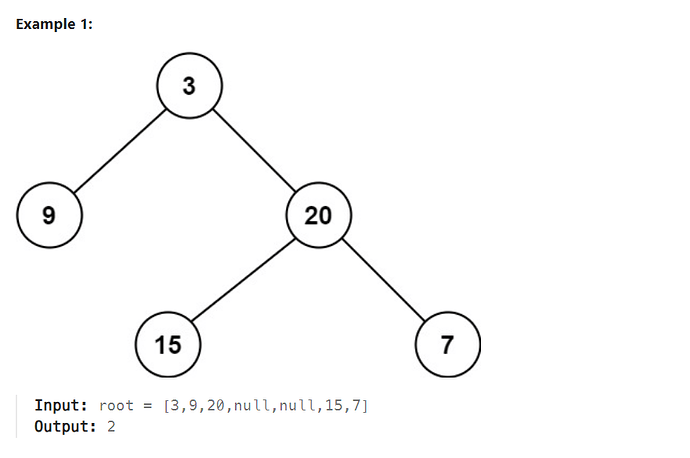
Example
思路
从Leetcode给我们的例子中可以看出来,我们需要获取到节点深度为最低的那个值,在第一个例子中,最低节点深度为2,从3到9
在第二个例子中,最低节点深度为5,因为它只有右孩子而没有左孩子。
那么问题来了,怎么去获取这个节点最低深度呢?
首先,先把当传入的节点为空条件写出来
!root 返回0;这是因为会有一个测试条件来传入空树。
然后我们就可以开始写另外一个函数来获取到最低深度了,这里需要用的是基本函数为min
getMinDepth(root)
让我们来写这么一个函数,返回值为int。
还是要写一个最基本的判断,跟上面的if一样。
这两个if有什么不同呢?
第一个if来接受题目传入的参数,如果为空直接结束了不会进入到我们的另外一个函数中。
第二个if,也就是我们的递归函数,递归函数最重要的一个条件就是写出结束条件,当为空,那么既是结束条件
写出了第一二个条件可以就可以思考接下来该怎么去写了。如果左右节点都为空的时候会发生什么呢?
左右节点都为空
如果发生以上情况树的深度会不会是1呢?答案是的,深度为1。因为只有一个头节点,一个头节点等于深度1
最后只需要使用min函数来获取到底是左还是右是最低深度了,这里就不多讲诉怎么去用min了。能进入到递归函数也就很明显的说明了这棵树最少深度会为2. 如果想不明白用笔在纸上试试看吧!
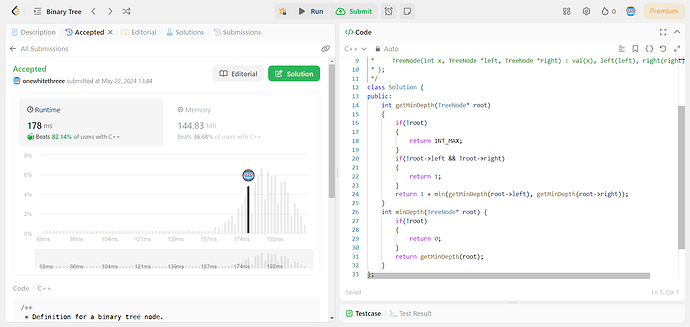
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getMinDepth(TreeNode* root)
{
if(!root)
{
return INT_MAX;
}
if(!root->left && !root->right)
{
return 1;
}
return 1 + min(getMinDepth(root->left), getMinDepth(root->right));
}
int minDepth(TreeNode* root) {
if(!root)
{
return 0;
}
return getMinDepth(root);
}
};
结束。