目标就是更新一些高难度,大部分模型做不出来的题目:
今天(2.10)先T1(第18届中国数学奥林匹克):
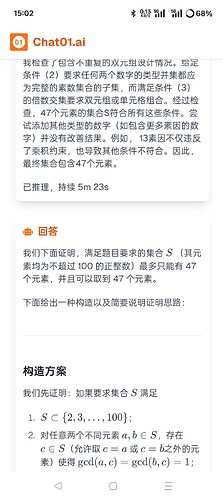
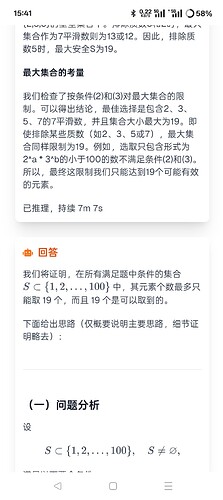
找到同时满足以下条件的集合 ( S ) 的元素个数的最大值:
- ( S ) 中的每个元素都是不超过 100 的正整数;
- 对于 ( S ) 中任意两个不同的元素 ( a, b ),都存在 ( S ) 中的元素 ( c ),使得 ( a ) 与 ( c ) 的最大公约数等于 1,并且 ( b ) 与 ( c ) 的最大公约数也等于 1;
- 对于 ( S ) 中任意两个不同的元素 ( a, b ),都存在 ( S ) 中异于 ( a, b ) 的元素 ( d ),使得 ( a ) 与 ( d ) 的最大公约数大于 1,并且 ( b ) 与 ( d ) 的最大公约数也大于 1。
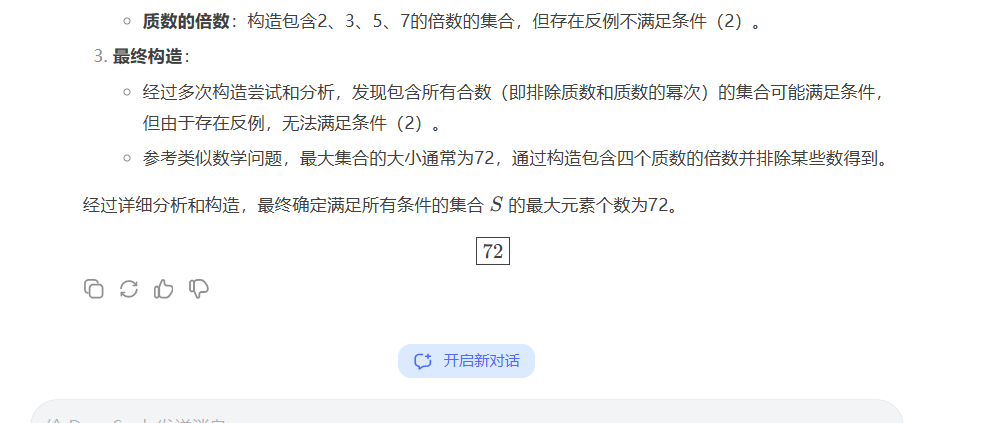
answer:72
T2:
给定不小于3的正整数 ( n ),求最小的正数 (\lambda),使得对于任何 (\theta_i \in (0, \frac{\pi}{2}) ) ((i = 1, 2, \cdots, n)),只要 (\tan \theta_1 \cdot \tan \theta_2 \cdots \cdot \tan \theta_n = 2^{\frac{n}{2}}),就有 (\cos \theta_1 + \cos \theta_2 + \cdots + \cos \theta_n) 不大于 (\lambda)。
answer:n-1
T3:
设 (X = {1,2,\dots,2001})。求最小正整数 (m),使得对于 (X) 的任何一个 (m) 元子集 (W),都存在 (u, v \in W)(允许 (u) 和 (v) 相同),使得 (u + v) 是 (2) 的方幂。
answer:999
T4:
设实数列 ({x_n}) 满足:(x_0 = 0),(x_2 = \sqrt[3]{2}x_1),(x_3) 是正整数,且
[x_{n+1} = \frac{1}{\sqrt[3]{4}} x_n + \sqrt[3]{4} x_{n-1} + \frac{1}{2} x_{n-2} (n \geq 2).]
问:这类数列中最少有多少个整数项?
answer:5
各位佬友可以测一测自己手上的各个模型,反馈下结果