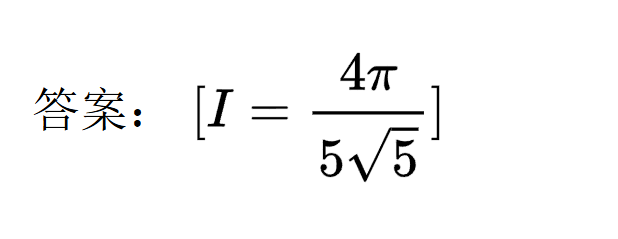49 个赞
其他模型不是不给答案就是给的答案是 0
2 个赞
帮帖主转换一下格式方便测试
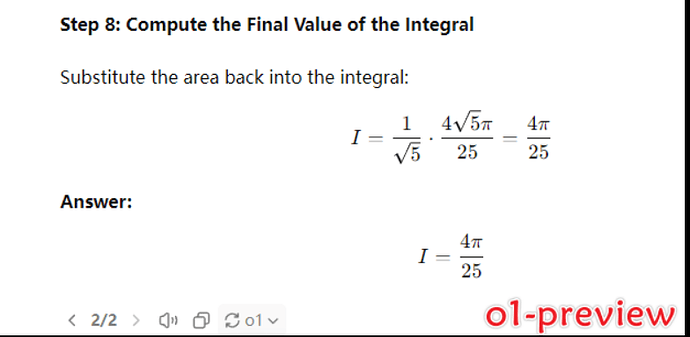
已知向曲线$L$ 是球面$x^2+y^2+z^2=2x$ 与平面$2x-z-1=0$的交线,从$z$轴正向往$z$轴负向看为逆时针方向,计算曲线积分
$$I=\int_L\left(6xyz-yz^2\right)\mathrm{d}x+2x^2z\mathrm{d}y+xyz\mathrm{d}z.$$
1 个赞
数一大佬!!
1 个赞
没考过 我只是测试一下
他这个只是答题比较牛逼吗?别的有没有提升啊,写代码啥的可以吗
1 个赞
o1-mini 写代码很行
1 个赞
我已经不会算了 ![]()
佬,公式怎么转成纯文字的?太神奇了。
国人开发的,个人用下来和mathpix差不多,支持图片和PDF,而且免费
8 个赞
谢谢佬,以后给孩子讲题自己就不用太累了。
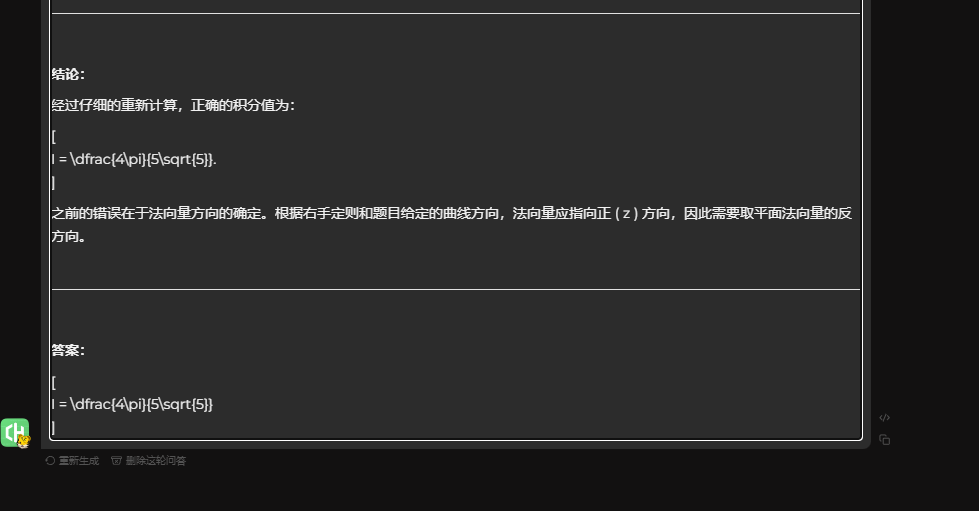
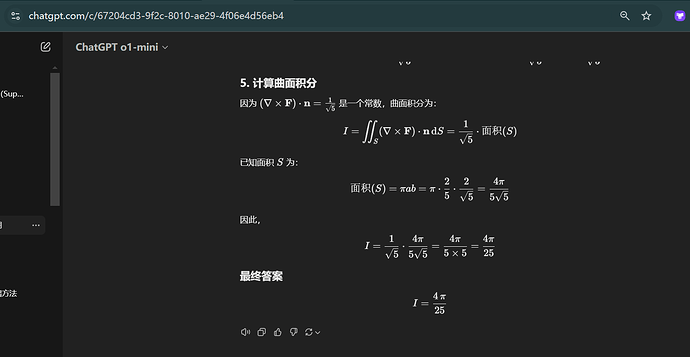
其实它也没有完全理解。点乘那一步是没有用的,正确答案没有负号。 \frac{4\sqrt{5}\pi}{25}
3 个赞
只能说这道题就是 O1 的上限了,还经常答不对
至于mini,怎么试都是错的