这道题有没有模型能作对。有没有佬试一下o1 pro

[yeahhe (Mozi)]

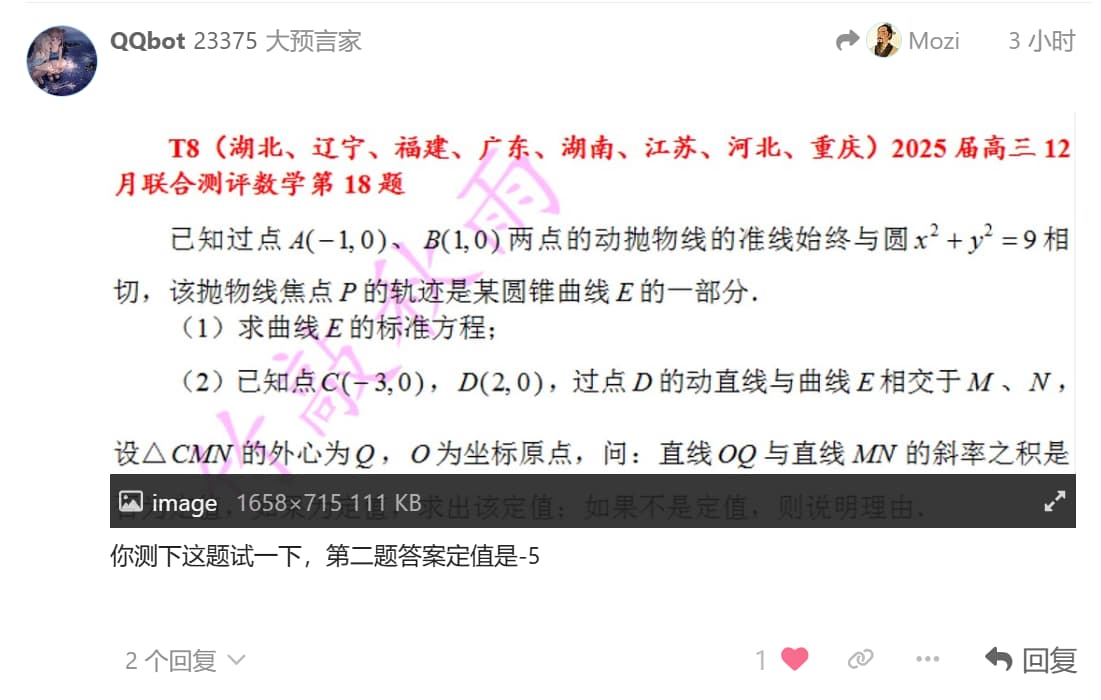
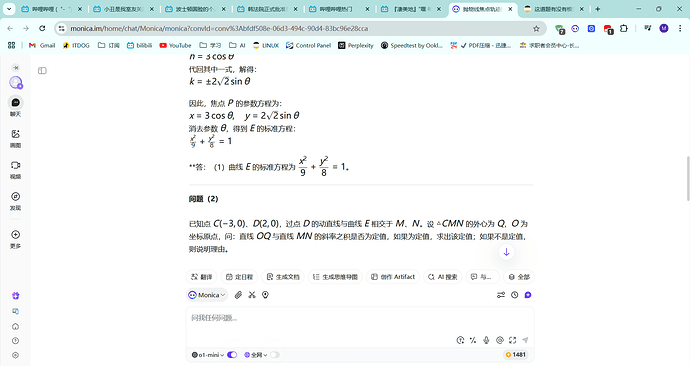
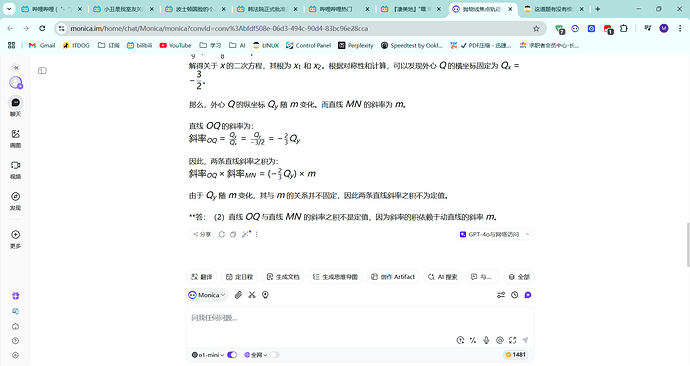
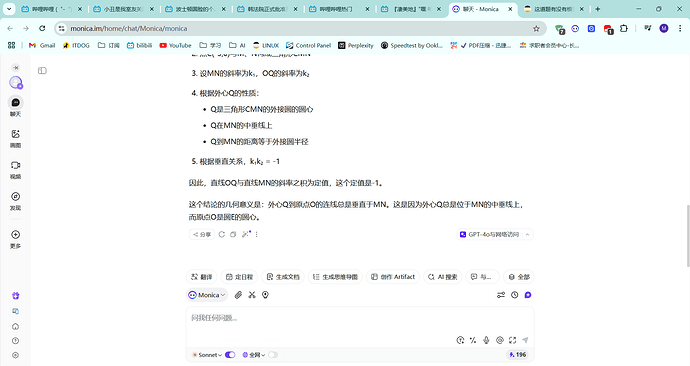
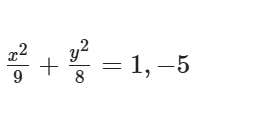已知过点 $A(-1, 0)$ 、 $B(1, 0)$ 两点的动抛物线的准线始终与圆 $x^2 + y^2 = 9$ 相切，该抛物线焦点 $P$ 的轨迹是某圆锥曲线 $E$ 的一部分。<br>(1) 求曲线 $E$ 的标准方程；<br>(2) 已知点 $C(-3, 0)$ ， $D(2, 0)$ ，过点 $D$ 的动直线与曲线 $E$ 相交于 $M$ 、 $N$ ，设 $\triangle CMN$ 的外心为 $Q$ ， $O$ 为坐标原点，问：直线 $OQ$ 与直线 $MN$ 的斜率之积是否为定值，如果为定值，求出该定值；如果不是定值，则说明理由。	

【长期更新Wiki】语言模型区分题库：主要用来区分语言模型，也能测试逻辑能力

序号 题型 题目 答案 1 解析几何 已知过点 $A(-1, 0)$ 、 $B(1, 0)$ 两点的动抛物线的准线始终与圆 $x^2 + y^2 = 9$ 相切，该抛物线焦点 $P$ 的轨迹是某圆锥曲线 $E$ 的一部分。<br>(1) 求曲线 $E$ 的标准方程；<br>(2) 已知点 $C(-3, 0)$ ， $D(2, 0)$ ，…

[lezishen (乐子神)]

[lezishen (乐子神)]

绝了
这么久

[yeahhe (Mozi)]

【长期更新Wiki】语言模型区分题库：主要用来区分语言模型，也能测试逻辑能力

序号 题型 题目 答案 1 解析几何 已知过点 $A(-1, 0)$ 、 $B(1, 0)$ 两点的动抛物线的准线始终与圆 $x^2 + y^2 = 9$ 相切，该抛物线焦点 $P$ 的轨迹是某圆锥曲线 $E$ 的一部分。<br>(1) 求曲线 $E$ 的标准方程；<br>(2) 已知点 $C(-3, 0)$ ， $D(2, 0)$ ，…

当然，目前这道题我能用的所有模型都做不对

[lezishen (乐子神)]

[taobao (淘宝)]

o1
第一问对了，第二问做错

[Jenhy (Agoni)]

gemini2.0的结果

[Simons (橘子苦)]

我会做，我是AI

[yeahhe (Mozi)]

来自佬给我的高考模拟卷

[lezishen (乐子神)]

[lezishen (乐子神)]

第一问做对了

[Jenhy (Agoni)]

全流程

[F-droid]

第一问没难度啊

[lezishen (乐子神)]

第二问都做错了

[Xcating]

o1-pro失败

[yeahhe (Mozi)]

有没有有o1 pro的佬，要不然就要看以后的新模型了

[yeahhe (Mozi)]

佬能多测几次吗，我没有o1 pro

[yeahhe (Mozi)]

o1 pro都做不对那就只能看以后有什么模型了，o3之类

[happyhome]

测试了一下，o1模型能做对，但第二题过程很简略

[F-droid]

好一个倒反天罡